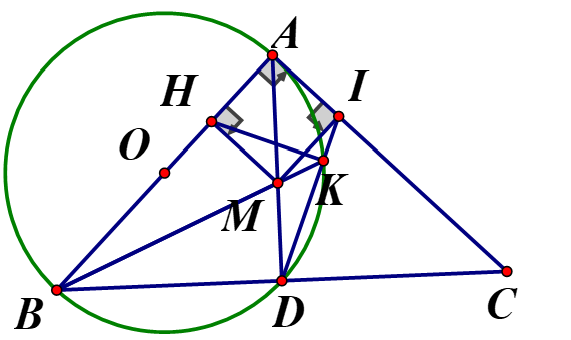
Cho tam giácABC Vuông cân đỉnh A .Đường tròn đường kính AD cắt BC tại D(D khác B).Điểm M bất kì trên đoạn AD ,kẻ MH, MI lần
50
07/05/2024
Cho tam giácABC Vuông cân đỉnh A .Đường tròn đường kính AD cắt BC tại D(D khác B).Điểm M bất kì trên đoạn AD ,kẻ MH, MI lần lượt vuông góc với AB và .
1) Chứng minh :Tứ giác nội tiếp;
2) Chứng minh :
3) Kẻ Chứng minh: thẳng hàng;
4) Khi M di động trên đoạn AD chứng minh rằng đường thẳngHK luôn đi qua một điểm có định
Trả lời
1, Vì là tứ giác nội tiếp
2) MDCI là tứ giác nội tiếp
vuông cân cũng vuông cân
là phân giác
cân tại A có AD phân giác nên cũng là đường trung trực
Từ (1) và (2) suy ra
3) Ta có : là tứ giác nội tiếp
Mà AHMI cũng nội tiếp nên thuộc một đường tròn
là tứ giác nội tiếp
Lại có : (MD là trung trực của
thẳng hàng.