Câu hỏi:
03/04/2024 40
Cho tam giác đều A1B1C1 có cạnh bằng a và có diện tích bằng S1. Nối các trung điểm của các cạnh tam giác A1B1C1 ta được tam giác A2B2C2 có diện tích là S2 tiếp tục như thế ta được dãy các tam giác. Tính a biết .
Cho tam giác đều A1B1C1 có cạnh bằng a và có diện tích bằng S1. Nối các trung điểm của các cạnh tam giác A1B1C1 ta được tam giác A2B2C2 có diện tích là S2 tiếp tục như thế ta được dãy các tam giác. Tính a biết .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Tỉ số diện tích của hai tam giác đồng dạng thì bằng bình phương tỉ số đồng dạng (1)
Công thức tính diện tích tam giác đều là:
(với x là độ dài cạnh tam giác) (2)
Từ (1) và (2) suy ra được:
;
.
Ta thấy S1, S2, S3,..., là các số hạng của một cấp số nhân lùi vô hạn có số hạng thứ nhất là và công bội .
Do đó
.
;
Mà
Do đó
Vậy a = 1.
Tỉ số diện tích của hai tam giác đồng dạng thì bằng bình phương tỉ số đồng dạng (1)
Công thức tính diện tích tam giác đều là:
(với x là độ dài cạnh tam giác) (2)
Từ (1) và (2) suy ra được:
;
.
Ta thấy S1, S2, S3,..., là các số hạng của một cấp số nhân lùi vô hạn có số hạng thứ nhất là và công bội .
Do đó
.
;
Mà
Do đó
Vậy a = 1.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hãy cho biết mệnh đề nào sau đây là sai? Hai đường thẳng vuông góc nếu:
Hãy cho biết mệnh đề nào sau đây là sai? Hai đường thẳng vuông góc nếu:
Câu 2:
Gọi φ là góc giữa 2 đường thẳng trong không gian. Chọn khẳng định đúng:
Câu 3:
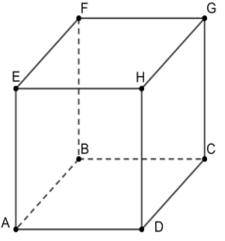
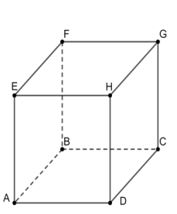
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính tích vô hướng bằng:

Câu 13:
Cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp vectơ và ?
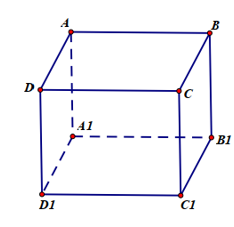
Cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp vectơ và ?

Câu 14:
Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M0(x0; y0) là
Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M0(x0; y0) là