Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12). Khi M thay đổi thì độ dài AM thay đổi
623
25/10/2023
Bài 9.8 trang 65 Toán 7 Tập 2:
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
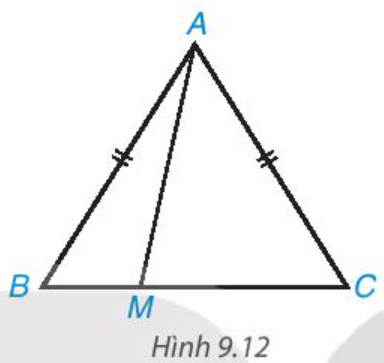 a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì AM < AB.
Trả lời
a) Kẻ AH vuông góc với BC tại H.
Khi M di chuyển trên BC thì tạo ra các đường xiên AM kẻ từ A xuống BC.
Trường hợp đặc biệt khi M trùng với H thì AM là đường vuông góc.
Mà trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Vậy M là chân đường cao kẻ từ A đến BC thì độ dài AM nhỏ nhất.
b)
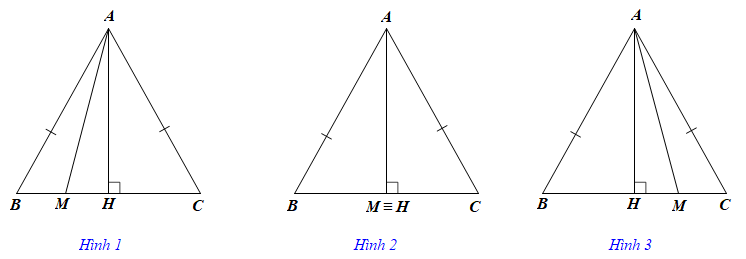
Ta xét các trường hợp sau:
• M nằm giữa B và H (Hình 1):
là góc tù nên ABM là tam giác tù.
Khi đó cạnh AB đối diện với là cạnh lớn nhất của ABM.
Hay AM < AB (1)
• M trùng với H (Hình 2):
AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ A đến BC.
Khi đó AH là đường ngắn nhất nên AH = AM < AB (2)
• M nằm giữa H và C (Hình 3):
là góc tù nên AMC là tam giác tù.
Khi đó cạnh AC đối diện với là cạnh lớn nhất của AMC.
Hay AM < AC
Mà AB = AC (do ABC cân tại A).
Do đó AM < AB (3)
Từ (1), (2) và (3) ta có AM < AB.
Vậy AM < AB.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 8
Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Bài 32: Quan hệ đường giữa đường vuông góc và đường xiên
Bài 33: Quan hệ giữa ba cạnh của một tam giác
Luyện tập chung trang 71
Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác
 a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
