Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của
20
30/10/2024
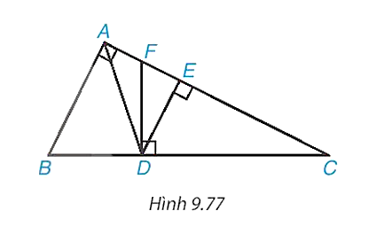
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC.
Chứng minh rằng:
a) BDBC=ABAB+AC, từ đó suy ra AE=AB⋅ACAB+AC;
Trả lời
a) Vì AD là tia phân giác của góc BAC nên BDDC=ABAC.
Suy ra BD . AC = DC . AB. (*)
Xét BD . (AB + AC) = BD . AB + BD . AC
= BD . AB + DC . AB (do (*))
= AB . (BD + DC)
= AB . BC.
Vậy BD . (AB + AC) = AB . BC. Suy ra BDBC=ABAB+AC. (1)
Hai tam giác CED vuông tại E và tam giác CAB vuông tại A có góc nhọn C chung nên
∆CED ∽ ∆CAB.
Suy ra CECA=CDCB⇒AC−AEAC=BC−BDBC⇒1−AEAC=1−DBBC.
Do đó, AEAC=DBBC. (2)
Từ (1) và (2) suy ra AEAC=ABAB+AC, do đó AE=AB⋅ACAB+AC.