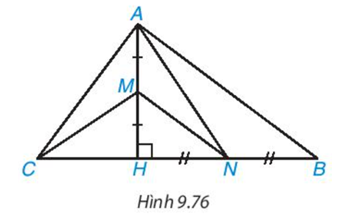
Cho tam giác ABC có đường cao AH. Biết AH = 12 cm, CH = 9 cm, BH = 16 cm. Lấy M, N lần lượt
18
30/10/2024
Cho tam giác ABC có đường cao AH. Biết AH = 12 cm, CH = 9 cm, BH = 16 cm. Lấy M, N lần lượt là trung điểm của AH, BH (H.9.76).
a) Chứng minh rằng ABC là tam giác vuông tại A.
Trả lời
a) Xét tam giác AHB vuông tại H, có:
AH2 + HB2 = AB2 (định lý Pythagore)
Suy ra AB2 = 122 + 162 = 400.
Suy ra AB = 20 cm.
Tương tự, có: AC2 = AH2 + CH2 (áp dụng định lý Pythagore trong tam giác vuông AHC).
Suy ra AC2 = 122 + 92 = 225.
Suy ra AC = 15 cm.
Có BC = CH + BH = 9 + 16 = 25 cm.
Trong tam giác ABC, nhận thấy AB2 + AC2 = BC2 (do 202 + 152 = 252 = 625).
Suy ra tam giác ABC vuông tại A (định lí Pythagore đảo).