Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng
7
16/11/2024
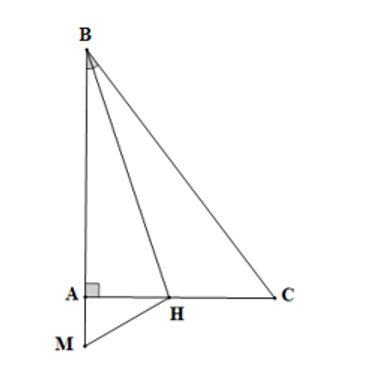
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
B. H là trực tâm tam giác MBC;
C. MH = HC;
D. Cả A, B, C đều sai.
Trả lời
Hướng dẫn giải
Đáp án đúng là: D
• Xét ΔBHM và ∆BHC có:
BH là cạnh chung,
(do BH là tia phân giác của góc ABC),
BM = BC (giả thiết)
Do đó ΔBHM = ∆BHC (c.g.c)
Suy ra MH = HC (hai cạnh tương ứng), nên C là khẳng định đúng.
• Vì BM = BC và HM = HC nên BH là đường trung trực của MC.
Do đó BH ⊥ MC hay BH là đường cao của tam giác MBC.
• Xét DBMC có hai đường cao BH và CA cắt nhau tại H nên H là trực tâm tam giác BMC. (Khẳng định B là đúng)
Do đó MH ⊥ BC nên khẳng định A là đúng.
Vậy ta chọn phương án D.