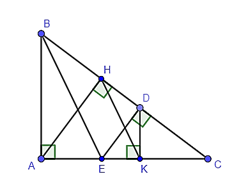
Cho tam giác ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE ⊥ DC (E ∈ AC), DK ⊥ AC (K ∈ AC). Khi đó BE song song với

Đáp án đúng là: C

Có DE ⊥ DC nên DE ⊥ BC (D ∈ BC).

Vì AH ⊥ BC nên AH // DE.

Lại có DK ⊥ AC , AB ⊥ AC nên DK // AB.

Xét tam giác ABC có DK // AB nên theo định lí Thalès ta có:

$\frac{\text{CD}}{\text{CB}}=\frac{\text{CK}}{\text{CA}}$(1)

Xét tam giác AHC có DE // AH nên theo định lí Thalès ta có:

$\frac{\text{CD}}{\text{CH}}=\frac{\text{CE}}{\text{CA}}$(2)

Chia theo vế (1) cho (2) ta được:

$\frac{\text{CD}}{\text{CB}}:\frac{\text{CD}}{\text{CH}}=\frac{\text{CK}}{\text{CA}}:\frac{\text{CE}}{\text{CA}}$

Suy ra $\frac{\text{CH}}{\text{CB}}=\frac{\text{CK}}{\text{CE}}$ .

Trong tam giác CEB có $\frac{\text{CH}}{\text{CB}}=\frac{\text{CK}}{\text{CE}}$   nên HK // BE (định lí Thaslès đảo).