Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 3 cm. Gọi M điểm di động trên cạnh BC sao cho MH vuông góc với AB tại H. Cho tam giác AHM quay quanh cạnh AH tạo nên một hình nón, thể tích lớn nhất của hình nón được tạo thành là

Đặt $AH=x\left(cm\right),0<x<6$

Khi đó $BH=6-x\left(cm\right)$

Xét tam giác BHM vuông tại H.

Ta có $\tan \widehat{HBM}=\frac{HM}{BH}$

$\Rightarrow HM=BH.\tan \widehat{HBM}=\left(6-x\right).\tan \widehat{HBM}$

Mà $\tan \widehat{HBM}=\tan \widehat{ABC}=\frac{AC}{AB}=\frac{3}{6}=\frac{1}{2}$

Do đó $HM=\left(6-x\right).\frac{1}{2}$

Thể tích của khối nón tạo thành khi tam giác AHM quay quanh cạnh AH là $V=\frac{1}{3}AH.\pi .H{M}^2=\frac{\pi }{3}.x.\frac{1}{4}{\left(6-x\right)}^2=\frac{\pi }{12}\left(x^3-12x^2+36x\right)$ (1).

Xét hàm số $f\left(x\right)=x^3-12x^2+36x$ với 0 < x < 6, ta có

$f^{\text{'}}\left(x\right)=3x^2-24x+36;\left(x\right)=0\iff 3x^2-24x+36=0\iff \left[\begin{array}{l}x=2\\ x=6\end{array}\right.$

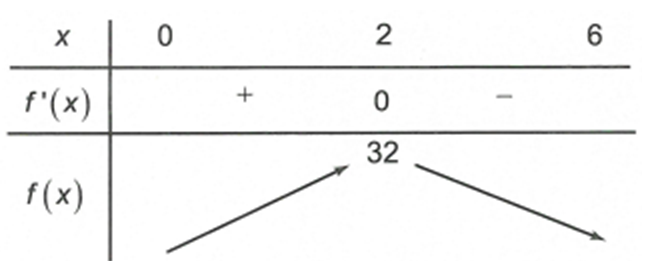
Bảng biến thiên của hàm số $f\left(x\right)=x^3-12x^2+36x$ với 0 < x < 6

Từ (1) và bảng biến thiên ta có thể tích lớn nhất của khối nón tạo thành là $V=\frac{\pi }{12}.32=\frac{8\pi }{3}$