Cho tam giác ABC nhọn, M là trung điểm BC và H là trực tâm của tam giác ABC. Đường thẳng qua H và vuông góc với MH cắt AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắ

16 10/11/2024

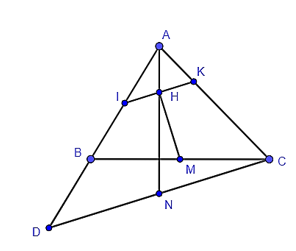
Cho tam giác ABC nhọn, M là trung điểm BC và H là trực tâm của tam giác ABC. Đường thẳng qua H và vuông góc với MH cắt AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắt AH và AB theo thứ tự tại N và D. Khẳng định nào sau đây là đúng?

A. NC = ND;

B. DB = NC;

C. Cả A, B đều sai

D. Cả A, B đều đúng.

Trả lời

Đáp án đúng là: A

Cho tam giác ABC nhọn, M là trung điểm BC và H là trực tâm của tam giác ABC. Đường thẳng qua H và vuông góc với MH cắt AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắt AH và AB theo thứ tự tại N và D. Khẳng định nào sau đây là đúng? A. NC = ND; B. DB = NC; C. Cả A, B đều sai; D. Cả A, B đều đúng. (ảnh 1)

Ta có AN ⊥ BC (do H là trực tâm của tam giác ABC) nên HN ⊥ CM (H ∈ AN, M ∈ BC).

Theo đề bài ta có IK // DC, IK ⊥ HM, do đó HM ⊥ DC hay HM ⊥ NC (N ∈ DC).

Tam giác HNC có: HM ⊥ NC, CM ⊥ HN.

Do đó M là trực tâm của tam giác HNC.

Suy ra MN ⊥ HC.

Lại có HC ⊥ AB nên MN // AB hay MN // DB.

Xét tam giác CBD có MN // DB nên theo định lí Thalès ta có:

$\frac{CM}{MB} = \frac{CN}{ND}$ hay $\frac{CN}{ND} = 1$ (Vì CM = MB, do M là trung điểm của BC)

Suy ra CN = ND.

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

Câu hỏi cùng chủ đề

Để tính chiều cao AB của một ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 4 m và biết được các khoảng cách BD = 7 m, DC = 5 m. Khi đó chiều cao AB của ngôi nhà là: A. 5,6

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

14 1 tháng trước

Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

15 1 tháng trước

Bóng của một tháp trên mặt đất có độ dài BC = 63 m. Cùng thời điểm đó, một cây cột DE cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m. Chiều cao của tháp là: A. 24 m; B. 42 m; C. 44 m; D

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

10 1 tháng trước

Giữa hai điểm B và C có một cái ao. Để đo khoảng cách BC người ta đo được các đoạn thẳng AD = 2 m, BD = 10 m và DE = 5 m. Biết DE // BC, tính khoảng cách giữa hai điểm B và C. A. 30 m; B. 2

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

15 1 tháng trước

Để đo khoảng cách giữa hai điểm A và B (không thể đo trực tiếp). Người ta xác định các điểm C, D, E như hình vẽ. Sau đó đo được khoảng cách giữa A và C là AC = 4 m, khoảng cách giữa C và E là

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

14 1 tháng trước

Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc CD đặt cố định vuông góc với mặt đất, với CD = 3 m và CA = 5 m. Sau đó, các bạn đã phố

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

20 1 tháng trước

Một cột đèn cao 15 m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 3 m và có bóng trải dài dưới mặt đất là 5 m. Tìm chiều cao của cây xanh. A. 5,793 m; B. 5,397 m; C. 9,573 m;

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

12 1 tháng trước

Cho hình vẽ dưới đây, biết cái cây có chiều cao ED = 2 m và khoảng cách AE = 4 m, EC = 2,5 m. Khi đó chiều cao AB của ngôi nhà là: A. AB = 5,2 m; B. AB = 3,2 m; C. AB = 1,25 m; D. AB = 3,5

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

11 1 tháng trước

Để đo chiều cao AC của một cột cờ, người ta cắm một cái cọc ED có chiều cao 2 m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5 m và khoảng cách AB là 9 m. Chiều

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

12 1 tháng trước

Bóng (AK) của một cột điện (MK) trên mặt đất dài 6 m. Cùng lúc đó một cột đèn giao thông (DE) cao 3 m có bóng (AE) dài 2 m. Chiều cao của cột điện (MK) là A. 8 m; B. 9 m; C. 1 m; D. 4 m.

Trắc nghiệm Toán 8 Bài 15. Định lí Thalès trong tam giác có đáp án

14 1 tháng trước

Xem tất cả

Cho tam giác ABC nhọn, M là trung điểm BC và H là trực tâm của tam giác ABC. Đường thẳng qua H và vuông góc với MH cắt AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắ

Trả lời

Câu hỏi cùng chủ đề

Để tính chiều cao AB của một ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 4 m và biết được các khoảng cách BD = 7 m, DC = 5 m. Khi đó chiều cao AB của ngôi nhà là: A. 5,6

Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2

Bóng của một tháp trên mặt đất có độ dài BC = 63 m. Cùng thời điểm đó, một cây cột DE cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m. Chiều cao của tháp là: A. 24 m; B. 42 m; C. 44 m; D

Giữa hai điểm B và C có một cái ao. Để đo khoảng cách BC người ta đo được các đoạn thẳng AD = 2 m, BD = 10 m và DE = 5 m. Biết DE // BC, tính khoảng cách giữa hai điểm B và C. A. 30 m; B. 2

Để đo khoảng cách giữa hai điểm A và B (không thể đo trực tiếp). Người ta xác định các điểm C, D, E như hình vẽ. Sau đó đo được khoảng cách giữa A và C là AC = 4 m, khoảng cách giữa C và E là

Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc CD đặt cố định vuông góc với mặt đất, với CD = 3 m và CA = 5 m. Sau đó, các bạn đã phố

Một cột đèn cao 15 m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 3 m và có bóng trải dài dưới mặt đất là 5 m. Tìm chiều cao của cây xanh. A. 5,793 m; B. 5,397 m; C. 9,573 m;

Cho hình vẽ dưới đây, biết cái cây có chiều cao ED = 2 m và khoảng cách AE = 4 m, EC = 2,5 m. Khi đó chiều cao AB của ngôi nhà là: A. AB = 5,2 m; B. AB = 3,2 m; C. AB = 1,25 m; D. AB = 3,5

Để đo chiều cao AC của một cột cờ, người ta cắm một cái cọc ED có chiều cao 2 m vuông góc với mặt đất. Đặt vị trí quan sát tại B, biết khoảng cách BE là 1,5 m và khoảng cách AB là 9 m. Chiều

Bóng (AK) của một cột điện (MK) trên mặt đất dài 6 m. Cùng lúc đó một cột đèn giao thông (DE) cao 3 m có bóng (AE) dài 2 m. Chiều cao của cột điện (MK) là A. 8 m; B. 9 m; C. 1 m; D. 4 m.

Danh mục