Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, AC. Khẳng định nào sau đây sai?

Đáp án đúng là: A

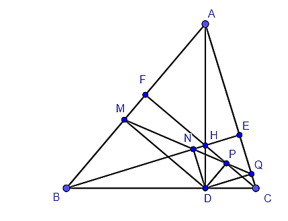
Ta có QD ⊥ AC, HE ⊥ AC (H ∈ BE) nên HE // QD hay BE // QD (H ∈ BE).

Xét tam giác ADQ có HE // DQ nên theo định lí Thalès ta có:  $\frac{\text{AE}}{\text{EQ}}=\frac{\text{AH}}{\text{HD}}$(1).

Có HF ⊥ AB (H ∈ CF), DM ⊥ AB nên HF // DM hay CF // DM.

Xét tam giác AMD có HF // DM nên theo định lí Thalès ta có: $\frac{\text{AF}}{\text{FM}}=\frac{\text{AH}}{\text{HD}}$  (2).

Từ (1) và (2) suy ra  $\frac{\text{AE}}{\text{EQ}}=\frac{\text{AF}}{\text{FM}}$.

Trong tam giác AMQ có  nên EF // MQ (định lí Thaslès đảo) (*).

Xét tam giác BFC có CF // DM nên theo định lí Thalès ta có: $\frac{\text{BM}}{\text{BF}}=\frac{\text{BD}}{\text{BC}}$  (3).

Có DN ⊥ BE, BE ⊥ EC (E ∈ AC) nên DN // CE.

Xét tam giác BEC có DN // CE nên theo định lí Thalès ta có: $\frac{\text{BN}}{\text{BE}}=\frac{\text{BD}}{\text{BC}}$  (4).

Từ (3) và (4) suy ra $\frac{\text{BM}}{\text{BF}}=\frac{\text{BN}}{\text{BE}}$ .

Trong tam giác BEF có $\frac{\text{BM}}{\text{BF}}=\frac{\text{BN}}{\text{BE}}$ nên MN // EF (định lí Thaslès đảo) (**).

Xét tam giác BEC có QD // BE nên theo định lí Thalès ta có: $\frac{\text{CQ}}{\text{QE}}=\frac{\text{CD}}{\text{DB}}$  (5).

Có DP ⊥ CF, BF ⊥ CF (F ∈ AB) nên DP // BF.

Xét tam giác BFC có  DP // BF nên theo định lí Thalès ta có:  $\frac{\text{CP}}{\text{PF}}=\frac{\text{CD}}{\text{DB}}$(6).

Từ (5) và (6) suy ra $\frac{\text{CQ}}{\text{QE}}=\frac{\text{CP}}{\text{PF}}$ .

Trong tam giác CEF có $\frac{\text{CQ}}{\text{QE}}=\frac{\text{CP}}{\text{PF}}$  nên PQ // EF (định lí Thaslès đảo)(***)

Từ (*), (**), (***) suy ra M, N, P, Q thẳng hàng.

Vậy A sai.