Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC
Bài 9.13 trang 69 Toán 7 Tập 2:
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
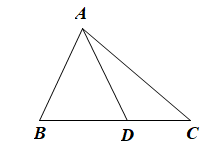
Trong tam giác ABD, theo bất đẳng thức tam giác ta có:
AD < AB + BD (1)
Trong tam giác ACD, theo bất đẳng thức tam giác ta có:
AD < AC + CD (2)
Từ (1) và (2) ta có:
AD + AD < AB + BD + AC + CD
Do đó 2AD < AB + AC + (BD + CD)
Hay 2AD < AB + AC + BC
Suy ra AD < (AB + AC + BC).
Mà chu vi tam giác ABC là AB + AC + BC.
Nên AD nhỏ hơn nửa chu vi tam giác ABC.
Vậy AD nhỏ hơn nửa chu vi tam giác ABC.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Bài 32: Quan hệ đường giữa đường vuông góc và đường xiên
Bài 33: Quan hệ giữa ba cạnh của một tam giác
Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác