Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.18)

Bài 9.12 trang 69 Toán 7 Tập 2:

Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.18).

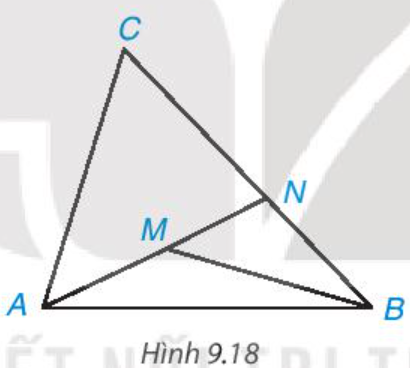a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB.

b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB.

c) Chứng minh MA + MB < CA + CB.

Trả lời

a) Áp dụng bất đẳng thức tam giác vào $∆$MNB có:

MB < MN + NB (độ dài một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại)

Cộng cả hai vế với MA ta được:

MA + MB < MA + MN + NB.

MA + MB < (MA + MN) + NB

Hay MA + MB < NA + NB.

b) Áp dụng bất đẳng thức tam giác vào $∆$ANC có:

NA < CA + CN (độ dài một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại)

Cộng cả hai vế với NB ta được:

 NA + NB < CA + CN + NB.

NA + NB < CA + (CN + NB)

Hay NA + NB < CA + CB.

c) Do MA + MB < NA + NB và NA + NB < CA + CB

Nên MA + MB < NA + NB < CA + CB.

Do đó MA + MB < CA + CB.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Bài 32: Quan hệ đường giữa đường vuông góc và đường xiên

Bài 33: Quan hệ giữa ba cạnh của một tam giác

Luyện tập chung trang 71

Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác