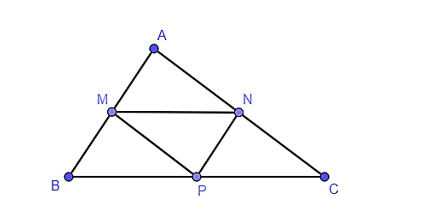
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?

A. 4;

B. 6;

Hướng dẫn giải:

Đáp án đúng là: D

Vì M, N lần lượt là trung điểm của AB, AC.

Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.

Vì M, P lần lượt là trung điểm của AB, BC.

Suy ra MP là đường trung bình của tam giác ABC nên MP // AC.

Vì N, P lần lượt là trung điểm của AC, BC.  

Suy ra NP là đường trung bình của tam giác ABC nên NP // AB.

Xét tam giác ABC:

+ Do MN // BC nên ΔAMN ᔕ ΔABC.

+ Do MP // AC nên ΔMBP ᔕ ΔABC.

+ Do NP // AB nên ΔNPC ᔕ ΔABC.

Vì ΔAMN ᔕ ΔABC, ΔMBP ᔕ ΔABC, ΔNPC ᔕ ΔABC nên các tam giác AMN, MBP, NPC đôi một đồng dạng với nhau.

Xét hai tam giác AMN và PNM có:

AM = PN $=\frac{1}{2}\text{AB}$

MN: Cạnh chung

MP = AN $=\frac{1}{2}\text{AC}$

Suy ra ΔAMN = ΔPNM (c – c – c).

Do đó, ΔAMN ᔕ ΔPNM.

Từ đó suy ra 5 tam giác AMN, PNM, MBP, NPC, ABC đôi một đồng dạng với nhau.

Vậy có tất cả 10 cặp tam giác đồng dạng.