Câu hỏi:
01/02/2024 47Cho tam giác ABC có I cách đều 3 đỉnh. Khi đó điểm I là
A. Một điểm bất kì nằm trong tam giác ABC;
B. Một điểm bất kì nằm trên đường trung trực của AB;
C. Một điểm bất kì nằm trên đường trung trực của AC;
D. Giao điểm của hai đường trung trực của AB và AC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
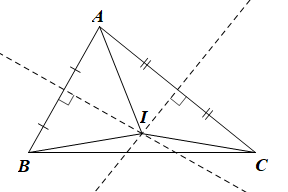
Do I cách đều 3 đỉnh của tam giác ABC nên I là giao điểm của ba đường trung trực của tam giác.
Hay I cũng là giao điểm của hai đường trung trực của AB và AC.
Vậy ta chọn phương án D.
Hướng dẫn giải
Đáp án đúng là: D

Do I cách đều 3 đỉnh của tam giác ABC nên I là giao điểm của ba đường trung trực của tam giác.
Hay I cũng là giao điểm của hai đường trung trực của AB và AC.
Vậy ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và AC. Kết quả nào dưới đây đúng?
Câu 2:
Cho các nhận xét sau:
(I) Giao điểm của ba đường trung trực trong một tam giác bất kì luôn nằm trong tam giác đó;
(II) Giao điểm của ba đường trung trực trong tam giác vuông nằm trên cạnh huyền của tam giác vuông đó;
(III) Giao điểm của ba đường trung trực trong tam giác nhọn nằm ngoài tam giác đó;
(IV) Giao điểm của ba đường trung trực trong tam giác tù nằm ngoài tam giác đó.
Có bao nhiêu nhận xét đúng?
Câu 4:
Cho các hình vẽ sau:
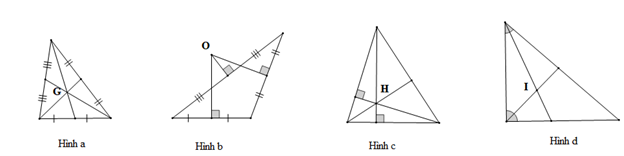
Hình nào có giao điểm của ba đường trung trực ?


