Câu hỏi:
30/01/2024 54Cho tam giác ABC, có AB = 2, BC = 7, AC = . Lấy M là trung điểm của AB, N là trung điểm của AC.
Độ dài đoạn thẳng MN là:
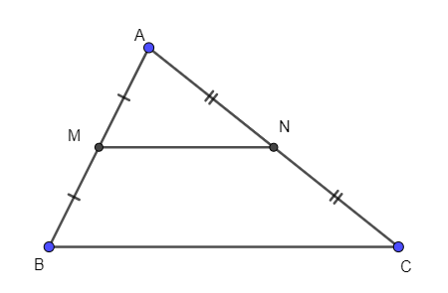
A. ;
A. ;
B. ;
B. ;
C. 3,5;
D. 6.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
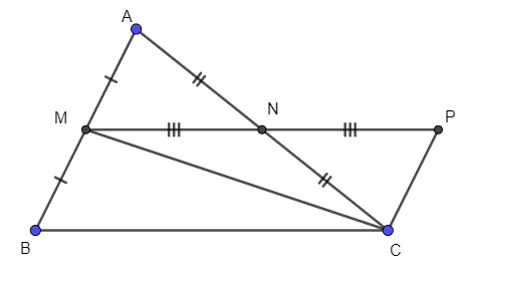
Trên tia đối của tia NM lấy điểm P sao cho MN = NP
⦁ Xét ∆ANM và ∆CNP, có:
AN = CN (gt)
(hai góc đối đỉnh)
MN = NP (cách dựng)
Do đó ∆ANM = ∆CNP (c – g – c)
⇒ AM = CP (hai cạnh tương ứng)
Mà AM = MB nên MB = CP
⇒ (hai góc tương ứng)
Mà hai góc ở vị trí so le trong nên AM // CP hay BM // CP
⇒ (hai góc so le trong)
⦁ Xét ∆BMC và ∆PCM, có:
MC là cạnh chung
(chứng minh trên)
BM = CP (chứng minh trên)
Do đó ∆BMC = ∆PCM (c – g – c)
⇒ BC = PM (hai cạnh tương ứng)
Mà MN = NP = MP
⇒ MN = BC = .7 = 3,5.
Hướng dẫn giải
Đáp án đúng là: C

Trên tia đối của tia NM lấy điểm P sao cho MN = NP
⦁ Xét ∆ANM và ∆CNP, có:
AN = CN (gt)
(hai góc đối đỉnh)
MN = NP (cách dựng)
Do đó ∆ANM = ∆CNP (c – g – c)
⇒ AM = CP (hai cạnh tương ứng)
Mà AM = MB nên MB = CP
⇒ (hai góc tương ứng)
Mà hai góc ở vị trí so le trong nên AM // CP hay BM // CP
⇒ (hai góc so le trong)
⦁ Xét ∆BMC và ∆PCM, có:
MC là cạnh chung
(chứng minh trên)
BM = CP (chứng minh trên)
Do đó ∆BMC = ∆PCM (c – g – c)
⇒ BC = PM (hai cạnh tương ứng)
Mà MN = NP = MP
⇒ MN = BC = .7 = 3,5.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho góc nhọn . Trên tia Ax lấy hai điểm B và E, trên tia Ay lấy hai điểm D và C sao cho AB = AD, AE = AC. Gọi O là giao điểm của DE và BC. Cho OC = 1,5 cm, OD = 1cm. Độ dài đoạn thẳng DE là:
Cho góc nhọn . Trên tia Ax lấy hai điểm B và E, trên tia Ay lấy hai điểm D và C sao cho AB = AD, AE = AC. Gọi O là giao điểm của DE và BC. Cho OC = 1,5 cm, OD = 1cm. Độ dài đoạn thẳng DE là:
Câu 2:
Cho ∆ABC có AB = AC. Trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho AD = AE. Gọi F là giao điểm của EB và DC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC có AB = AC. Trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho AD = AE. Gọi F là giao điểm của EB và DC. Khẳng định nào sau đây đúng nhất?


