Cho phương trình $4^{-|x-m|}.{\log }_{\sqrt{2}}\left(x^2-2x+3\right)+2^{2x-x^2}.{\log }_{\frac{1}{2}}\left(2\right|x-m|+2)=0$ với m là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là

A. 4. 

B. 1.

C. 2.

D. 3.

Phương trình đã cho tương đương với phương trình
$2^{-2|x-m|+1}.{\log }_2\left(x^2-2x+3\right)-2^{2x-x^2}.{\log }_2\left(2\right|x-m|+2)=0$
$\iff 2^{-2}|x-m|+1.{\log }_2\left(x^2-2x+3\right)=2^{2x-x^2}.{\log }_2\left(2\right|x-m|+2)$
$\iff 2^{x^2-2x}.{\log }_2\left(x^2-2x+3\right)=2^2|x-m|-1.{\log }_2\left(2\right|x-m|+2).$
Xét hàm số $f\left(t\right)=2^{t-3}.{\log }_{2}t$ với $t\ge 2.$ Do $t\ge 2$ suy ra ${\log }_{2}t\ge 1.$
Ta có: $f^{\text{'}}\left(t\right)=2^{t-3}.\frac{1}{t.\ln 2}+2^{t-3}.\ln 2.{\log }_{2}t>0$ với $t\ge 2.$
Do đó hàm số $f\left(t\right)$ đồng biến trên $[2;+\infty )$
$\Rightarrow f\left(x^2-2x+3\right)=f\left(2\right|x-m|+2)\iff x^2-2x+3=2|x-m|+2$
$\iff |x-m|=\frac{x^2}{2}-x+\frac{1}{2}\iff \left[\begin{array}{l}m=\frac{-x^2}{2}+2x-\frac{1}{2}\\ m=\frac{x^2}{2}+\frac{1}{2}\end{array}(*).\right.$
Vẽ đồ thị các hàm số $y=\frac{-x^2}{2}+2x-\frac{1}{2}$ và $y=\frac{x^2}{2}+\frac{1}{2}$ trên cùng một hệ trục tọa độ.

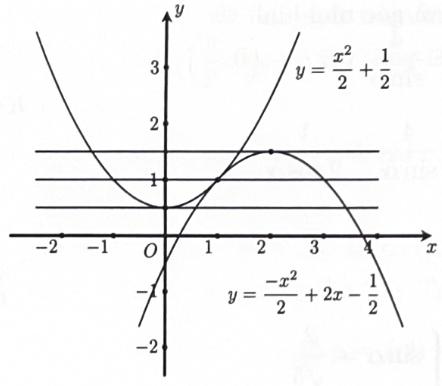
Đồ thị hai hàm số tiếp xúc với nhau tại điểm (1;1). Điểm cực trị của đồ thị hàm số $y=\frac{x^2}{2}+\frac{1}{2}$ là $\left(0;\frac{1}{2}\right),$ điểm cực trị của đồ thị hàm số $y=\frac{-x^2}{2}+2x-\frac{1}{2}$ là $\left(2;\frac{3}{2}\right).$
Dựa vào đồ thị, để (*) có ba nghiệm phân biệt thì $m\in \left\{\frac{1}{2};1;\frac{3}{2}\right\}.$
Tổng tất cả các giá trị của tham số m thỏa màn là $\frac{1}{2}+1+\frac{3}{2}=3.$

Chọn D