Cho nữa đường tròn tâm O đường kính ABC là một điểm nằm giữa O và A . Đường thẳng vuông góc với AB Tại C cắt nữa đườn tròn trên
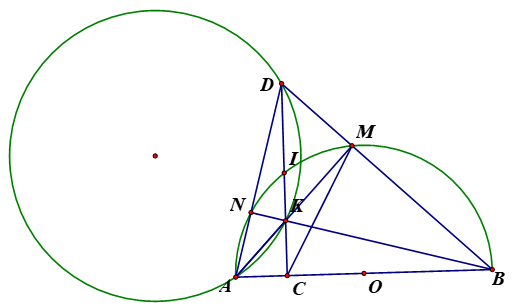
Cho nữa đường tròn tâm O đường kính ABC là một điểm nằm giữa O và A . Đường thẳng vuông góc với AB Tại C cắt nữa đườn tròn trên tại IK là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nữa đường tròn (O) tại M tia BM cắt tia CI tại D Chứng minh:
1) Các tứ giác : ACMD;BCKM nội tiếp đường tròn .
2) CK.CD=CA.CB
3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B,K,N thẳng hàng.
4) Tâm đường tròn ngoại tiếp tam giác AKD Nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI