Cho nữa đường tròn tâm O đường kính AB và điểm M bất kì trên nữa đường tròn ( M khác A và B) .Trên nữa mặt phẳng bờ AB chứa nữa
49
07/05/2024
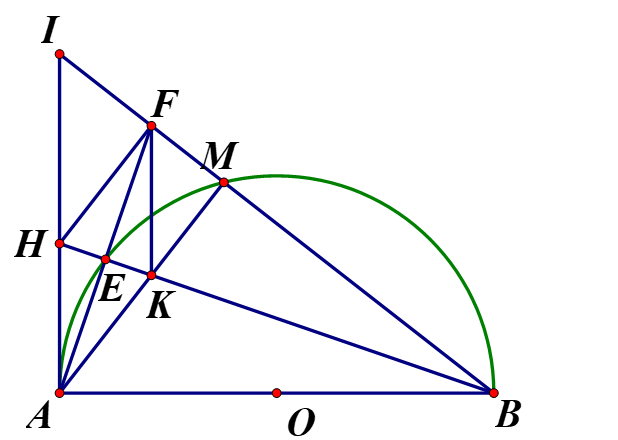
Cho nữa đường tròn tâm O đường kính AB và điểm M bất kì trên nữa đường tròn ( M khác A và B) .Trên nữa mặt phẳng bờ AB chứa nữa đường tròn kẻ tiếp tuyến Ax .Tia BM cắt Ax tại I tia phân giác của góc IAM cắt nữa đường tròn tại E cắt tia BM tại F Tia BE cắt Ax tại H cắt AM tại K
1. Chứng minh rằng : Là tư giác nội tiếp và
2. Chứng minh BEF là tam giác cân
3 .Chứng minh rằng tư giác là hình thoi
Trả lời
Tứ giác nội tiếp AEMB , vì
Ax là tiếp tuyến của
là góc nội tiếp chắn đường tròn
là tam giác vuông tại A, AM đường cao
2) là góc tạo bởi tia tiếp tuyến và dây cung chắn AE
là góc nội tiếp chắn
Ta có: AF là phân giác
Lại có:và là hai góc nội tiếp lần lượt chắn cung nên là đường phân giác
là góc nội tiếp chắn đường tròn
là đường cao
là tam giác cân tại B (vì BE vừa là đường cao, vừa là đường phân giác)
3) cân tại B, BFlà đường cao là đường trung trực của AF
AFlà tia phân giác có AEvừa là đường cao, vừa là đường phân giác cân tại A
Từ (1) và (2) suy ra là hình thoi