Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, a ⊥ (P). Giả sử điểm M thỏa mãn
Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, a ⊥ (P). Giả sử điểm M thỏa mãn OM ⊥ (P). Chứng minh rằng M ∈ a.
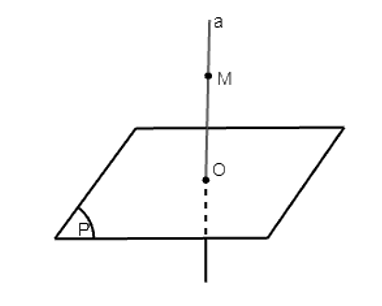
Ta có a ⊥ (P) tại O.
Mặt khác, có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước, tức là tồn tại duy nhất đường thẳng a đi qua điểm O và vuông góc với mặt phẳng (P).
Nên nếu OM ⊥ (P) thì M ∈ a.