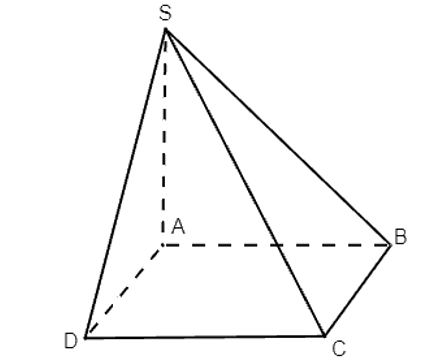
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông.

Ta có: SA ⊥ (ABCD), BC ⊂ (ABCD) và DC ⊂ (ABCD).

Suy ra: SA ⊥ BC và SA ⊥ DC.

Vì ABCD là hình chữ nhật nên BC ⊥ AB và DC ⊥ AD.

· Ta có: BC ⊥ SA, BC ⊥ AB và SA ∩ AB = A trong (SAB).

Suy ra BC ⊥ (SAB).

Mà SB ⊂ (SAB) nên BC ⊥ SB hay tam giác SBC vuông tại B.

· Ta có: DC ⊥ AD, DC ⊥ SA và AD ∩ SA = A trong (SAD).

Suy ra DC ⊥ (SAD).

Mà SD ⊂ (SAD) nên DC ⊥ SD hay tam giác SCD vuông tại D.