Ta có thể tích khối nón đỉnh S lớn hơn hoặc bằng thể tích khối nón đỉnh S'. Do đó chỉ cần xét khối nón đỉnh S có bán kính đường tròn đáy là r và đường cao là SI = h với $h\ge R$. Thể tích khối nón được tạo nên bởi (N) là

$$\begin{gathered} V=\frac{1}{3}h{S}_{\left(C\right)}=\frac{1}{3}h.\pi .r^2 \\ =\frac{1}{3}.h.\pi \left[R^2-{\left(h-R\right)}^2\right] \\ =\frac{1}{3}\pi \left(-h^3+2h^{2}R\right) \end{gathered}$$

Xét hàm số $f\left(h\right)=-h^3+2h^{2}R$ với $h\in \left[R;2R\right)$

Ta có $f^{\text{'}}\left(h\right)=-3h^2+4hR$

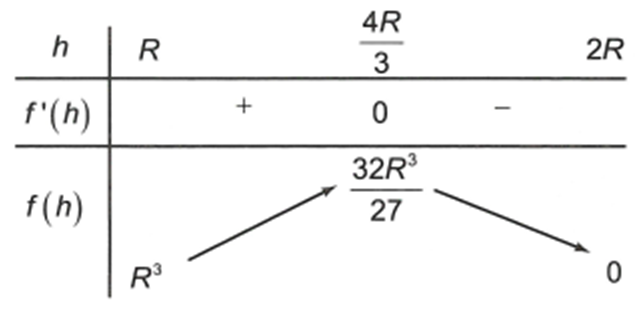
$f^{\text{'}}\left(h\right)=0\iff -3h^2+4hR=0\iff h=0$ (loại) hoặc $h=\frac{4R}{3}$

Bảng biến thiên

Ta có $\max f\left(h\right)=\frac{32}{27}{R}^3$ tại $h=\frac{4R}{3}$

Vậy thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất là $V=\frac{1}{3}\pi \frac{32}{27}{R}^3=\frac{32}{81}\pi R^3$ khi $h=\frac{4R}{3}$