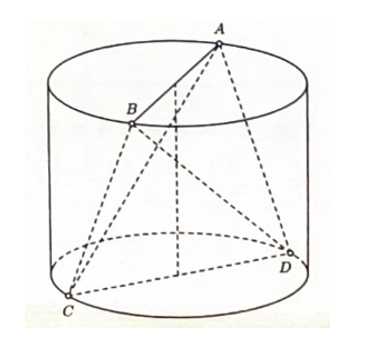
Cho khối trụ (T), AB và CD lần lượt là hai đường kính trên các mặt đáy của khối (T).

Cho khối trụ (T), AB và CD lần lượt là hai đường kính trên các mặt đáy của khối (T). Biết góc giữa AB và CD là 30°, AB = 6cm và thể tích khối ABCD là 30cm³. Khi đó thể tích khối trụ (T) là

Trả lời

Gọi h, V lần lượt là chiều cao và thể tích khối trụ (T)

$\Rightarrow d(AB,CD)=h( \text{cm})\text{. }$

Ta có: $V_{ABCD}=\frac{1}{6}h.\sin (AB;CD).AB.CD=\frac{1}{6}h.\sin 30°{.6}^2$

$\Rightarrow h=\frac{6V_{ABCD}}{\sin {30}^{°}\cdot 6^2}=10( \text{cm})\text{. }$

$\Rightarrow V_{\left(T\right)}=\pi {\left(\frac{AB}{2}\right)}^2.h=90\pi \left({\text{cm}}^3\right).$

Chọn A