Cho khối chóp đều S.ABCD có AB = 2a và thể tích bằng 4 căn bậc hai 3 / 3 a^3Côsin góc giữa hai mặt phẳng (SAB) và (SCD) bằng

Cho khối chóp đều S.ABCD có AB = 2a và thể tích bằng $\frac{4\sqrt{3}}{3}{a}^3.$ Côsin góc giữa hai mặt phẳng (SAB) và (SCD) bằng

C. $\frac{1}{\sqrt{3}}.$                 

Trả lời

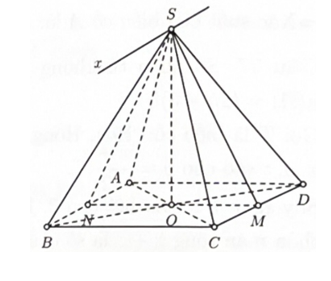
Cho khối chóp đều S.ABCD có O là tâm hình vuông ABCD như hình vẽ.

Ta có $S_{ABCD}=4a^2;V_{S.ABCD}=\frac{1}{3}{S}_{ABCD}.SO$ 

$\Rightarrow SO=a\sqrt{3}.$

Mặt khác $AB//CD$

$\Rightarrow \left(SAB\right)\cap \left(SCD\right)=Sx//AB//CD\text{. }$

Gọi M, N lần lượt là trung điểm của CD và AB.

$SN\perp AB\Rightarrow SN\perp Sx,SM\perp CD\Rightarrow SM\perp Sx.$

$\Rightarrow \left(\right(SAB),(SCD\left)\right)=(SM,SN)=\widehat{MSN}=2\widehat{MSO}.$

Ta có $\tan \widehat{MSO}=\frac{OM}{SO}=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{MSO}={30}^{°}\Rightarrow \widehat{MSN}={60}^{°}\Rightarrow \cos \widehat{MSN}=\frac{1}{2}\text{. }$

Chọn B