Câu hỏi:
03/04/2024 51Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mp(P) // mp(SBC). Thiết diện tạo bởi mp (P) và hình chóp S.ABCD là hình gì?
A. Hình vuông
B. Hình thang
C. Tam giác
D. Hình bình hành
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
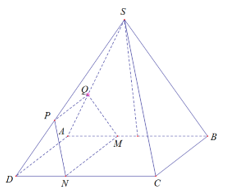
Trong mặt phẳng (ABCD) kẻ Mx song song với BC
Mx cắt CD tại N
MN // (SBC) (1)
Trong mặt phẳng (SCD) kẻ Ny song song với SC
Ny cắt SD tại P
NP // (SBC) (2)
Trong mặt phẳng (SAB) kẻ Mz song song với SB
Mz cắt SA tại Q
MQ // (SBC) (3)
Từ (1), (2), (3), ta có thiết diện MNPQ tạo bởi mặt phẳng (P) và hình chóp S.ABCD
Xét tứ diện MNPQ có:
PQ // ADPQ // MN
MNPQ là hình thang
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Hình nào sau đây là có thể là hình biểu diễn của hình hộp chữ nhật trong không gian:
Câu 4:
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mặt phẳng (P). Gọi M là điểm nằm giữa S và A; N là điểm nằm giữa S và B; giao điểm của hai đường thẳng AC và BD là O; giao điểm của hai đường thẳng CM và SO là I; giao điểm của hai đường thẳng NI và SD là J. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN) là:
Câu 7:
Cho hình chóp SABCD có đáy là một hình bình hành. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tìm mệnh đề đúng trong các mệnh đề sau:
Câu 8:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I,J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:
Câu 9:
Cho tứ diện đều S.ABC cạnh bằng a. Gọi I là trung điểm AB, M là một điểm di động trên đoạn AI. Qua M vẽ mặt phẳng () song song với (SIC). Thiết diện tạo bởi () và tứ diện SABC là
Câu 10:
Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ 4 đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại 4 điểm A’, B’, C’, D’. Tứ giác A’B’C’D’ là hình gì?
Câu 11:
Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Hỏi nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có bao nhiêu đường thẳng đi qua M cắt cả a và b.
Câu 12:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là:
Câu 13:
Cho tứ diện ABCD và 3 điểm I, J, K lần lượt nằm trên 3 cạnh AC, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (IJK) là:
Câu 14:
Cho tứ diện đều ABCD có cạnh bằng a,điểm M trên cạnh AB sao cho AM=m(0<m<a). Khi đó diện tích thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
Câu 15:
Cho hình chóp S.ABCD. Một mặt phẳng không đi qua đỉnh nào của hình chóp cắt các cạnh SA,SB,SC,SD lần lượt tại A’,B’,C’,D’. Gọi O là giao điểm của AC và BD. Tìm mệnh đề đúng trong các mệnh đề sau:


