Câu hỏi:
29/01/2024 63
Cho hình vẽ dưới đây. Giả thiết: Ax // Cy.
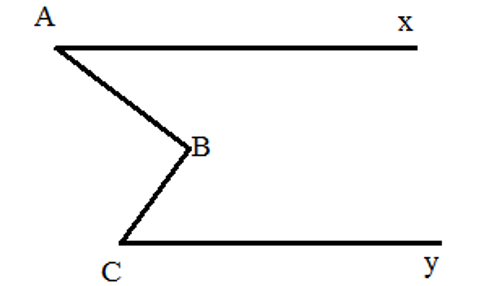
Kết luận đúng là
Cho hình vẽ dưới đây. Giả thiết: Ax // Cy.

Kết luận đúng là
A. ^BCy−^xAB=^ABC
B. 2^BCy−2^xAB=^ABC
C. ^xAB2+^BCy2=^ABC
D. ^xAB+^BCy=^ABC
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Qua B, kẻ đường thẳng mn song song với đường thẳng chứa tia Ax.
Kẻ đường thẳng EF (E thuộc Ax, F thuộc Cy) cắt mn tại K.
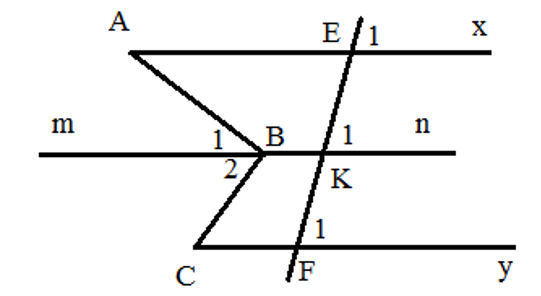
Vì Ax // mn nên ^xAB=^B1 (hai góc so le trong) (1)
Vì Ax // mn nên ^E1=^K1 (hai góc đồng vị)
mà Ax // Cy (gt) nên ^E1=^F1 (hai góc đồng vị)
Suy ra ^E1=^K1 mà chúng ở vị trí đồng vị
Do đó: mn // Cy.
Vì mn // Cy nên ^BCy=^B2 (hai góc so le trong) (2)
Từ (1) và (2) ta có: ^xAB+^BCy=^B1+^B2
Mà ^ABC=^B1+^B2
Vậy ^xAB+^BCy=^ABC.
Hướng dẫn giải
Đáp án đúng là: D
Qua B, kẻ đường thẳng mn song song với đường thẳng chứa tia Ax.
Kẻ đường thẳng EF (E thuộc Ax, F thuộc Cy) cắt mn tại K.

Vì Ax // mn nên ^xAB=^B1 (hai góc so le trong) (1)
Vì Ax // mn nên ^E1=^K1 (hai góc đồng vị)
mà Ax // Cy (gt) nên ^E1=^F1 (hai góc đồng vị)
Suy ra ^E1=^K1 mà chúng ở vị trí đồng vị
Do đó: mn // Cy.
Vì mn // Cy nên ^BCy=^B2 (hai góc so le trong) (2)
Từ (1) và (2) ta có: ^xAB+^BCy=^B1+^B2
Mà ^ABC=^B1+^B2
Vậy ^xAB+^BCy=^ABC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình vẽ. Giả thiết: Hq là tia phân giác góc rHp, Hn là tia phân giác góc mHp.
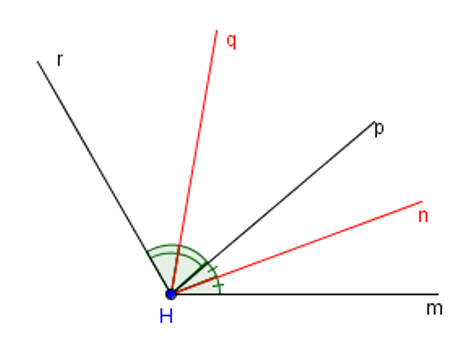
Kết luận đúng là
Cho hình vẽ. Giả thiết: Hq là tia phân giác góc rHp, Hn là tia phân giác góc mHp.

Kết luận đúng là
Câu 2:
Cho hình vẽ.
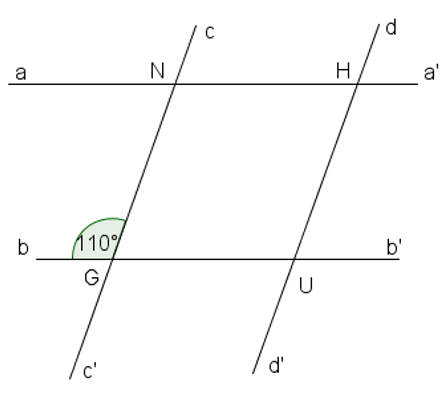
Giả thiết: aa' // bb', cc' // dd' và ^bGN=110°. Kết luận đúng là
Cho hình vẽ.

Giả thiết: aa' // bb', cc' // dd' và ^bGN=110°. Kết luận đúng là


