Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:AC² + BD² = 4(OA² + OB²) = 4AB².

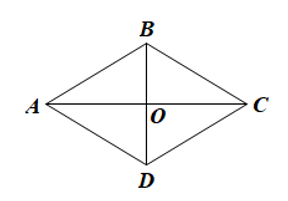
Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Do đó AC = 2OA, BD = 2OB.

Ta có: AC² + BD² = (2OA)² + (2OB)² = 4OA² + 4OB² = 4(OA² + OB²).

Xét ΔOAB vuông tại O, theo định lí Pythagore ta có:

AB² = OA² + OB²

Suy ra AC² + BD² = 4(OA² + OB²) = 4AB².