Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao

Bài 1.20 trang 29 Chuyên đề Toán 11: Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao của hai đường chéo. Tìm ảnh của đoạn thẳng AB qua các phép vị tự V_{(O, 2)}, V_{(I, – 2)}.

Trả lời

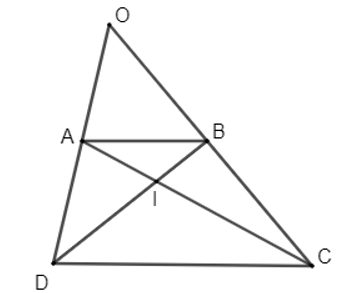
+ Vì ABCD là hình thang có hai đáy AB và CD nên AB // CD. Theo định lí Thales trong tam giác OCD ta có: $\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{CD}=\frac{1}{2}$.

Suy ra $\overrightarrow{OD}=2\overrightarrow{OA};\overrightarrow{OC}=2\overrightarrow{OB}$.

Do đó, D và C tương ứng là ảnh của A và B qua phép vị tự V_{(O, 2)}. Vậy đoạn thẳng DC là ảnh của đoạn thẳng AB qua phép vị tự V_{(O, 2)}.

+ Vì AB // CD nên theo hệ quả của định lí Thales trong tam giác ICD ta có:

$\frac{IA}{IC}=\frac{IB}{ID}=\frac{AB}{CD}=\frac{1}{2}$.

Suy ra $\overrightarrow{IC}=-2\overrightarrow{IA};\overrightarrow{ID}=-2\overrightarrow{IB}$.

Do đó, C và D tương ứng là ảnh của A và B qua phép vị tự V_{(I, – 2)}. Vậy đoạn thẳng CD là ảnh của đoạn thẳng AB qua phép vị tự V_{(I, – 2)}.

Xem thêm các bài giải Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác: