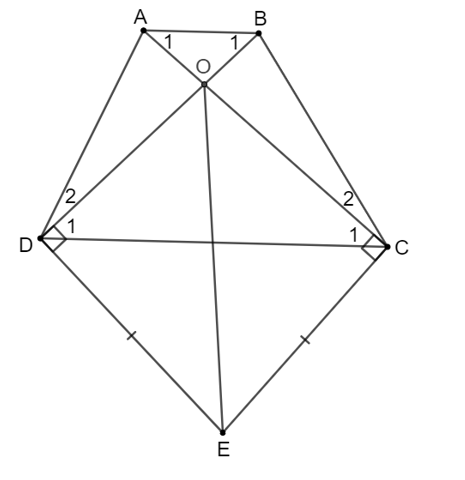
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Gọi O là giao điểm của AC và BD.

Xét ∆DOE và ∆COE có:

$\widehat{ODE}=\widehat{OCE}=90°$ (vì OD ⊥ DE; OC ⊥ CE)

EC = ED (giả thiết)

Cạnh OE chung

Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).

Suy ra OC = OD (hai cạnh tương ứng).

Do đó tam giác OCD cân tại O nên ${\widehat{C}}_1={\widehat{D}}_1$.

Vì ABCD là hình thang nên AB // CD suy ra ${\widehat{A}}_1={\widehat{C}}_1;{\widehat{B}}_1={\widehat{D}}_1$ (cặp góc so le trong).

Do đó ${\widehat{A}}_1={\widehat{B}}_1$ (vì ${\widehat{C}}_1={\widehat{D}}_1$).

Suy ra tam giác OAB cân tại O nên OA = OB.

Xét ∆OAD và ∆OBC có:

OA = OB (chứng minh trên)

$\widehat{AOD}=\widehat{BOC}$ (hai góc đối đỉnh)

OC = OD (chứng minh trên)

Do đó ∆OAD = ∆OBC (c.g.c)

Suy ra ${\widehat{C}}_2={\widehat{D}}_2$ (hai góc tương ứng).

Ta có $\widehat{ADC}={\widehat{D}}_1+{\widehat{D}}_2;\widehat{BCD}={\widehat{C}}_1+{\widehat{C}}_2$.

Mà ${\widehat{C}}_1={\widehat{D}}_1 ;{\widehat{C}}_2={\widehat{D}}_2$ nên $\widehat{ADC}=\widehat{BCD}$.

Hình thang ABCD có $\widehat{ADC}=\widehat{BCD}$ nên ABCD là hình thang cân.