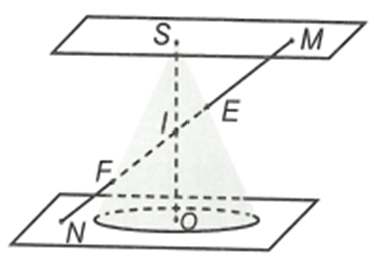
Cho hình nón tròn xoay nằm giữa hai mặt phẳng song song (P) và (Q) như hình vẽ. Kẻ đường cao SO của hình nón và gọi I là trung điểm của SO.
61
21/04/2024
Cho hình nón tròn xoay nằm giữa hai mặt phẳng song song (P) và (Q) như hình vẽ. Kẻ đường cao SO của hình nón và gọi I là trung điểm của SO. Lấy và đi qua I cắt mặt nón tại E và F đồng thời tạo với SO một góc 45o. Biết góc giữa đường cao và đường sinh của hình nón bằng . Độ dài đoạn EF là
A.
B.
C.
D.
Trả lời
Chọn B
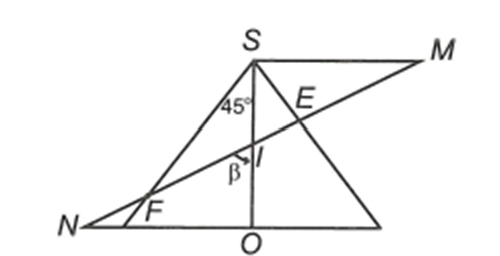
Xét tam giác NIO có
Xét tam giác SEF vuông tại S có
Vì SI là độ dài đường phân giác trong góc nên
Do đó


