Câu hỏi:
01/02/2024 51Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông \(\left( {\widehat A = \widehat B = 90^\circ } \right).\) Có bao nhiêu góc vuông tại đỉnh A thuộc các mặt của lăng trụ?
A. 0;
B. 1;
C. 2;
D. 3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
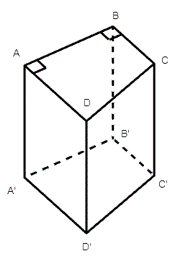
Do ABCD là hình thang vuông \(\left( {\widehat A = \widehat B = 90^\circ } \right)\) nên ta có \(\widehat {BAD} = 90^\circ .\)
Mặt khác ta có hình lăng trụ đứng ABCD.A'B'C'D' nên ta có: \(\widehat {A'AD} = 90^\circ ,\) \(\widehat {BAA'} = 90^\circ \).
Vậy có ba góc vuông tại đỉnh A thuộc các mặt của lăng trụ đứng là \(\widehat {BAD},\)\(\widehat {A'AD},\) \(\widehat {BAA'}.\)
Hướng dẫn giải
Đáp án đúng là: D

Do ABCD là hình thang vuông \(\left( {\widehat A = \widehat B = 90^\circ } \right)\) nên ta có \(\widehat {BAD} = 90^\circ .\)
Mặt khác ta có hình lăng trụ đứng ABCD.A'B'C'D' nên ta có: \(\widehat {A'AD} = 90^\circ ,\) \(\widehat {BAA'} = 90^\circ \).
Vậy có ba góc vuông tại đỉnh A thuộc các mặt của lăng trụ đứng là \(\widehat {BAD},\)\(\widehat {A'AD},\) \(\widehat {BAA'}.\)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một hình lăng trụ đứng có tất cả 5 mặt. Hình lăng trụ này có bao nhiêu đỉnh?
Câu 2:
Hình lăng trụ đứng tứ giác có:
(1) Các mặt đáy song song với nhau;
(2) Các mặt đáy là tam giác;
(3) Các mặt đáy là tứ giác;
(4) Các mặt bên là hình chữ nhật.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
Câu 3:
Cho một hình lăng trụ đứng có tổng 12 cạnh. Hỏi đáy của hình lăng trụ đứng này không thể là hình gì?
Câu 4:
Cho hình lăng trụ đứng ABCD.EHGF có đáy ABCD là hình thang cân (AB // CD). Có bao nhiêu cạnh có độ dài bằng với độ dài cạnh GH?
Câu 5:
Cho lăng trụ đứng tứ giác ABCD.EFGH, biết CD = 4 cm và diện tích của mặt CDHG bằng 36 cm2. Chiều cao của lăng trụ là:
Câu 6:
Cho hình lăng trụ đứng sau:
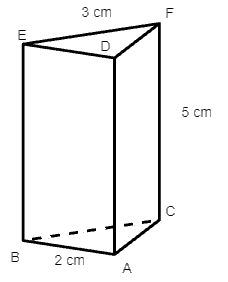
Độ dài của các cạnh ED, BC, DA lần lượt bằng


