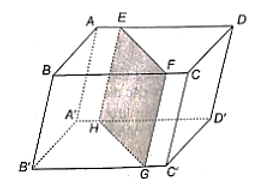
Cho hình hộp ABCD.A'B'C'D'. Một mặt phẳng (P) cắt các cạnh AD, BC, B'C', A'D' lần lượt tại E, F, G, H. Chứng minh rằng tứ giác EFGH là hình bình hành.
Cho hình hộp ABCD.A'B'C'D'. Một mặt phẳng (P) cắt các cạnh AD, BC, B'C', A'D' lần lượt tại E, F, G, H. Chứng minh rằng tứ giác EFGH là hình bình hành.