Cho hình hộp ABCD.A'B'C'D'. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng
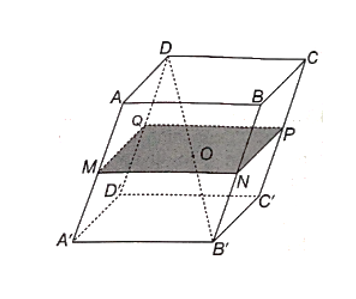
Cho hình hộp ABCD.A'B'C'D'. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng (ABCD) cắt các cạnh AA', BB', CC', DD' lần lượt tại M, N, P, Q.
a) Chứng minh rằng M, N, P, Q lần lượt là trung điểm của các cạnh AA', BB', CC', DD'.