Cho hình chữ nhật ABCD tâm I, biết AB = 2a. Gọi J là trung điểm BC, đường thẳng qua I và vuông góc

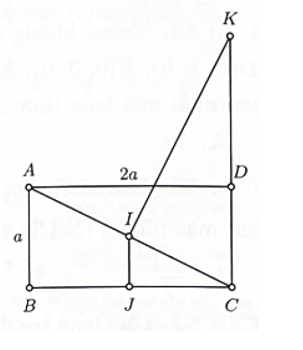
Cho hình chữ nhật ABCD tâm I, biết AB = 2a. Gọi J là trung điểm BC, đường thẳng qua I và vuông góc với AC cắt CD tại K. Thể tích V của khối tròn xoay tạo thành khi cho tứ giác CKIJ quay xung quanh trục CK bằng

B. $\frac{7}{6}\pi a^3.$

Trả lời

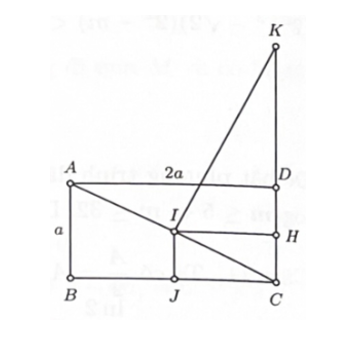
Gọi H là trung điểm CD nên tứ giác CHIJ là hình chữ nhật. Khi cho tứ giác CKIJ quay xung quanh trục CK ta có: Hình chữ nhật CHIJ tạo thành khối trụ có thể tích $V_1.$ Tam giác IHK tạo thành khối nón có thể tích $V_2.$

Suy ra: $V=V_1+V_2.$Ta có

$V_1=\pi .C{J}^2.CH=\pi a^2.\frac{a}{2}=\frac{1}{2}\pi a^3,$

$V_2=\frac{1}{3}\pi .H{I}^2.HK=\frac{1}{3}\pi a^2.HK.$

Xét tam giác vuông IHC có $IC=\sqrt{I{H}^2+H{C}^2}=\frac{a\sqrt{5}}{2};$

$\tan \widehat{ICH}=\frac{IH}{CH}=2\Rightarrow IK=IC.\tan \widehat{ICH}=2.\frac{a\sqrt{5}}{2}=a\sqrt{5}$

$\Rightarrow HK=\sqrt{I{K}^2-I{H}^2}=\sqrt{5a^2-a^2}=2a.$

Do vậy $V_2=\frac{1}{3}\pi .H{I}^2.HK=\frac{1}{3}\pi a^2.2a=\frac{2}{3}\pi a^3.$

Vậy $V=V_1+V_2=\frac{1}{2}\pi a^3+\frac{2}{3}\pi a^3=\frac{7}{6}\pi a^3.$

Chọn B