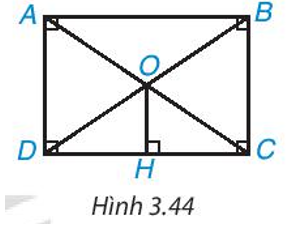
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.

Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Suy ra OA = OB = OC = OD.

Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.

Do đó CH = DH.

Vậy H là trung điểm của DC.