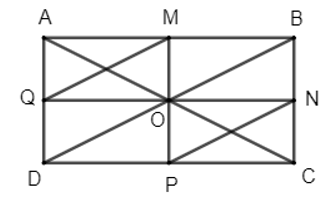
a) Vì O là giao hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có M và O lần lượt là trung điểm của AB và AC nên MO là đường trung bình của tam giác ABC, suy ra MO // BC và MO = BC (1).
Xét tam giác DBC có O và P lần lượt là trung điểm của BD và DC nên OP là đường trung bình của tam giác DBC, suy ra OP // BC và OP = BC (2).
Từ (1) và (2) suy ra O, P, M thẳng hàng và OM = OP nên O là trung điểm của PM.
Chứng minh tương tự ta được O là trung điểm của QN.
Do đó, ta có phép đối xứng tâm O biến các điểm A, M, Q tương ứng thành các điểm C, P, N.
Như vậy, phép đối xứng tâm O biến tam giác AMQ thành tam giác CPN.
b) Ta có QN // AB // CD và AD ⊥ AB nên AD ⊥ QN, mà Q là trung điểm của AD nên QN là đường trung trực của đoạn thẳng AD.
Ta có AD // MP nên QN ⊥ MP, mà O là trung điểm của MP nên QN là đường trung trực của đoạn thẳng MP.
Do đó, ta có phép đối xứng trục QN biến các điểm A, M, O tương ứng thành các điểm D, P, O.
Như vậy, phép đối xứng trục QN biến tam giác AMO thành tam giác DPO (3).
Ta lại có: , do đó ta có phép tịnh tiến theo vectơ biến các điểm D, P, O tương ứng thành các điểm P, C, N. Khi đó, phép tịnh tiến theo vectơ biến tam giác DPO thành tam giác PCN (4).
Từ (3) và (4) ta suy ra phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng trục QN và phép tịnh tiến theo vectơ (ĐQN trước, sau) biến tam giác AMO thành tam giác PCN.