Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.

Trả lời

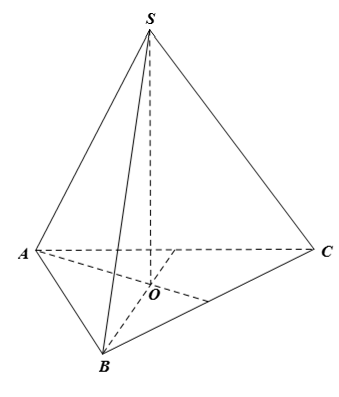
Do S.ABC là hình chóp tam giác đều nên SA = SB = SC (các cạnh bên bằng nhau).

Gọi O là chân đường cao của hình chóp tam giác đều S.ABC.

Do SO ⊥ (ABC) nên SO ⊥ OA, SO ⊥ OB, SO ⊥ OC.

Xét ∆SAO và ∆SBO có:

$\widehat{SOA}=\widehat{SOB}=90°;$

SO là cạnh chung;

SA = SB (chứng minh trên)

Do đó ∆SAO = ∆SBO (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{SAO}=\widehat{SCO}$ (hai góc tương ứng)

Chứng minh tương tự, ta cũng có∆SAO = ∆SCO nên $\widehat{SAO}=\widehat{SCO}.$ 

Từ đó ta có: $\widehat{SAO}=\widehat{SBO}=\widehat{SCO}.$

Vậy các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.