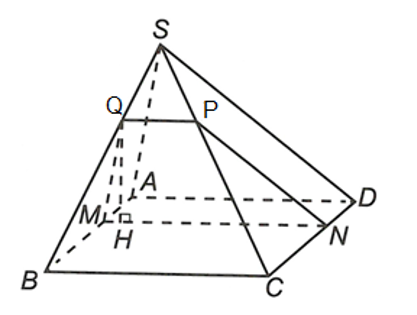
Cho hình chóp SABCD với ABCD là hình thoi cạnh a, tam giác SAD đều. M là điểm trên cạnh AB, (α) là mặt phẳng qua M và (α) // (SAD) cắt CD, SC, SD lần lượt tại N, P, Q.

a) Chứng minh rằng MNPQ là hình thang cân.

Do (α) đi qua M và (α) // (SAD) nên (α) cắt các mặt của hình chóp tại các giao tuyến song song với (SAD).

+) Trong mặt phẳng (ABCD), từ điểm M kẻ đường thẳng song song với AD cắt CD tại N. Suy ra giao tuyến của (α) và (ABCD) là MN // AD.

+) Trong mặt phẳng (SCD), từ điểm N kẻ đường thẳng song song với SD cắt SC tại P. Suy ra giao tuyến của (α) và (SCD) là NP // SD.

+) Trong mặt phẳng (SBC), từ điểm P kẻ đường thẳng song song với BC // AD cắt SB tại Q. Suy ra giao tuyến của (α) và (SBC) là PQ // AD.

+) Trong mặt phẳng (SAB), nối M và Q. Suy ra giao tuyến của (α) và (SAB) là MQ // SA.

a) Xét từ giác MNPQ, có: MN // PQ nên MNPQ là hình thang.

Ta có: SA // MQ, MN // AD và  $\widehat{SAD}=60°$ nên  $\widehat{QMN}=60°$.

Ta lại có: MN // AD, NP // SD và  $\widehat{SDA}=60°$ nên  $\widehat{PNM}=60°$.

Suy ra:  $\widehat{QMN}=\widehat{PNM}=60°$

Do đó tứ giác MNPQ là hình thang.