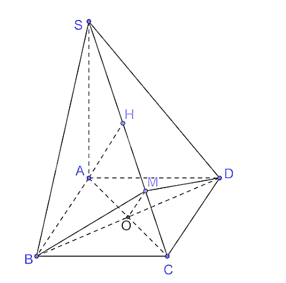
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC ⊥ (MBD) và AH // (MBD).
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC ⊥ (MBD) và AH // (MBD).