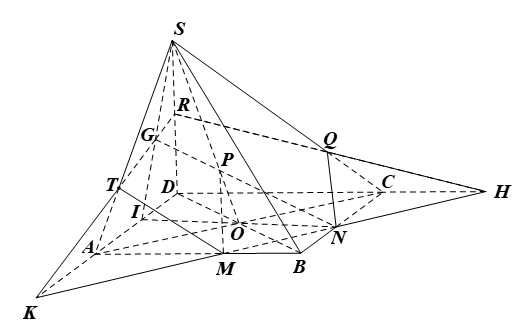
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm của AC và BD. Gọi M, N, P lần lượt là ba điểm nằm trên các cạnh AB, BC, SO. Xác định giao tuyến của mặt phẳng (MNP) với cá
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm của AC và BD. Gọi M, N, P lần lượt là ba điểm nằm trên các cạnh AB, BC, SO. Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình chóp S.ABCD (nếu có).