Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36). a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC. b) Xác định hình chiếu của đường
16
20/10/2024
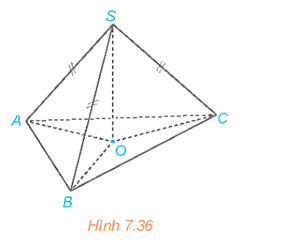
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
Trả lời
a) Vì O là hình chiếu của S trên mặt phẳng (ABC) nên SO ^ (ABC), suy ra SO ^ OA, SO ^ OB, SO ^ OC.
Xét tam giác SOA vuông tại O, có SO2 + OA2 = SA2.
Xét tam giác SOB vuông tại O, có SO2 + OB2 = SB2.
Xét tam giác SOC vuông tại O, có SO2 + OC2 = SC2.
Mà SA = SB = SC nên OA = OB = OC hay O là tâm đường tròn ngoại tiếp tam giác ABC.
b) O là hình chiếu của S trên mặt phẳng (ABC), A là hình chiếu của A trên mặt phẳng (ABC). Do đó OA là hình chiếu của SA trên mặt phẳng (ABC).