Cho hình chóp đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các đoạn thẳng SA, SB, SC. Chứng minh rằng phần hình
12
10/11/2024
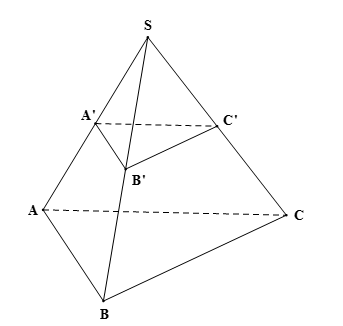
Cho hình chóp đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các đoạn thẳng SA, SB, SC. Chứng minh rằng phần hình chóp đã cho giới hạn bởi hai mặt phẳng (ABC) và (A’B’C’) là hình chóp cụt đều.
Trả lời
⦁ Xét ∆SAB có: A’, B’ lần lượt là trung điểm của SA, SB nên A’B’ là đường trung bình của ∆SAB. Do đó A’B’ // AB.
Mà AB ⊂ (ABC).
Suy ra A’B’ // (ABC).
⦁ Chứng minh tương tự, ta cũng có B’C’ // (ABC).
Ta có: A’B’ // (ABC), B’C’ // (ABC) và A’B’ ∩ B’C’ = B’ trong (A’B’C’).
Suy ra (A’B’C’) // (ABC).
Mà S.ABC là hình chóp đều.
Vậy phần hình chóp đã cho giới hạn bởi hai mặt phẳng (ABC) và (A’B’C’) là hình chóp cụt đều.