Câu hỏi:
12/03/2024 51
Cho hình bình hành ABCD. Lấy một điểm S nằm ngoài mặt phẳng (ABCD). Giao tuyến của (ACD) và (SAB) và đường thẳng CD
Cho hình bình hành ABCD. Lấy một điểm S nằm ngoài mặt phẳng (ABCD). Giao tuyến của (ACD) và (SAB) và đường thẳng CD
A. Song song với nhau;
B. Trùng nhau;
D. Cắt nhau.
D. Cắt nhau.
D. Cắt nhau.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
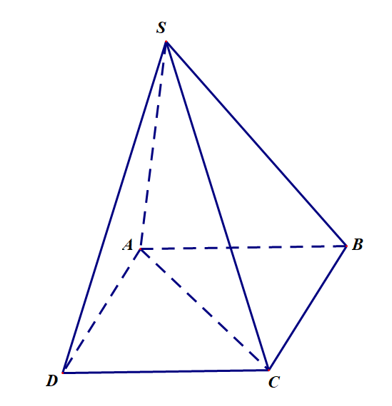
Vì A, B, C, D cùng nằm trên mặt phẳng (ABCD) nên giao tuyến của (SAB) và (ACD) chính là giao tuyến của (SAB) và (ABCD) hay chính là đường thẳng AB.
Do ABCD là hình bình hành nên hai đường thẳng AB và CD song song với nhau.
Đáp án đúng là: A

Vì A, B, C, D cùng nằm trên mặt phẳng (ABCD) nên giao tuyến của (SAB) và (ACD) chính là giao tuyến của (SAB) và (ABCD) hay chính là đường thẳng AB.
Do ABCD là hình bình hành nên hai đường thẳng AB và CD song song với nhau.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai đường thẳng chéo nhau a và b. Lấy và . Hai đường thẳng AD và BC
Cho hai đường thẳng chéo nhau a và b. Lấy và . Hai đường thẳng AD và BC
Câu 2:
Trong không gian có 3 đường thẳng a, b và c chéo nhau từng đôi một. Số đường thẳng có thể cắt cả 3 đường thẳng này là
Trong không gian có 3 đường thẳng a, b và c chéo nhau từng đôi một. Số đường thẳng có thể cắt cả 3 đường thẳng này là
Câu 3:
Có 3 đường thẳng phân biệt a, b, c; a và b song song với nhau. Khẳng định sai trong các khẳng định sau là
Có 3 đường thẳng phân biệt a, b, c; a và b song song với nhau. Khẳng định sai trong các khẳng định sau là
Câu 5:
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng
Câu 6:
Điểm phân biệt giữa hai đường thẳng song song và hai đường thẳng chéo nhau là
Điểm phân biệt giữa hai đường thẳng song song và hai đường thẳng chéo nhau là
Câu 8:
Cho 3 đường thẳng a, b, c. Biết a và b song song, a và c chéo nhau. Khi đó b và c
Cho 3 đường thẳng a, b, c. Biết a và b song song, a và c chéo nhau. Khi đó b và c


