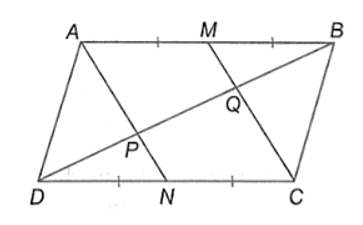
Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: DP = PQ = QB.
Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: DP = PQ = QB.