Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có vecto MA + veto MC = veto MB + vecto MD

Bài 4.34 trang 72 Toán 10 Tập 1: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có: 

$\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$

Trả lời

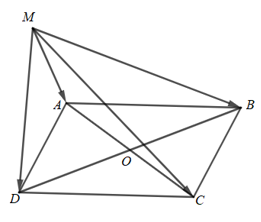
Gọi O là giao điểm của AC và BD.

Suy ra O là trung điểm của AC và BD.

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$ và $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$

Ta có:

+) 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OC} \\ =2\overrightarrow{MO}+\left(\overrightarrow{OA}+\overrightarrow{OC}\right)=2\overrightarrow{MO} \end{gathered}$$

(Vì $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$)

+) 

$$\begin{gathered} \overrightarrow{MB}+\overrightarrow{MD}=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD} \\ =2\overrightarrow{MO}+\left(\overrightarrow{OB}+\overrightarrow{OD}\right)=2\overrightarrow{MO} \end{gathered}$$

 (Vì $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$)

Suy ra $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}.$

Vậy $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}.$

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng. Đo độ phân tán