Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình

32 20/05/2024

Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.

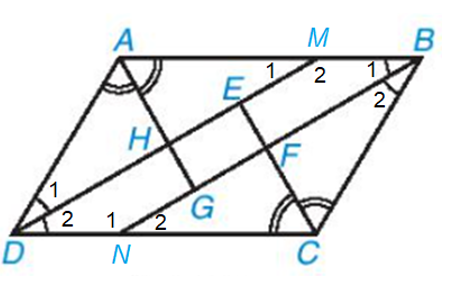
Vì tứ giác ABCD là hình bình hành nên AB // CD hay AM // DN.

Suy ra ${\hat{M}}_{1} = {\hat{D}}_{2}$ (hai góc so le trong)

Mà ${\hat{D}}_{1} = {\hat{D}}_{2}$ (vì DM là tia phân giác $\hat{A D C}$ ).

Do đó ${\hat{M}}_{1} = {\hat{D}}_{1}$ nên tam giác ADM cân tại A.

Chứng minh tương tự, ta có tam giác BCN cân tại C.

Vì ${\hat{B}}_{1} = {\hat{B}}_{2}; {\hat{D}}_{1} = {\hat{D}}_{2}$ (vì DM, BN lần lượt là tia phân giác của $\hat{A D C}; \hat{A B C}$ ).

Mà $\hat{A D C} = \hat{A B C}$ (vì tứ giác ABCD là hình bình hành).

Do đó ${\hat{B}}_{1} = {\hat{B}}_{2} = {\hat{D}}_{1} = {\hat{D}}_{2}$ .

Tam giác ADM cân tại A, tam giác BCN cân tại C.

Mà ${\hat{B}}_{1} = {\hat{D}}_{2}$ nên ${\hat{M}}_{1} = {\hat{N}}_{2}$ suy ra ${\hat{M}}_{1} = {\hat{N}}_{2}$ .

Tứ giác BMDN có ${\hat{B}}_{1} = {\hat{D}}_{2}; {\hat{M}}_{2} = {\hat{N}}_{1}$ nên tứ giác BMDN là hình bình hành.

Suy ra DM // BN hay HE // GF.

Tam giác ADM cân tại A có AH là đường phân giác nên AH cũng là đường cao.

Suy ra $\hat{A H E} = 90 °$ nên $\hat{E H G} = 90 °$ .

Mà HE // GF suy ra $\hat{A G F} = 90 °$ (hai góc đồng vị).

Tương tự, ta cũng chứng minh được: $\hat{H E F} = 90 °; \hat{G F E} = 90 °$ .

Tứ giác EFGH có $\hat{E H G} = 90 °; \hat{A G F} = 90 °; \hat{H E F} = 90 °; \hat{G F E} = 90 °$ .

Do đó tứ giác EFGH là hình chữ nhật.

Xem tất cả