Cho hàm số y=f(x)=ã^3+bx^2+cx+d ( a,b,c,d thuộc R) có đồ thị như hình bên.
Cho hàm số y=f(x)=ax3+bx2+cx+d (a,b,c,d∈ℝ) có đồ thị như hình bên. Đặt y=g(x)=f(x2+x+2) .
Chọn khẳng định đúng trong các khẳng định sau.
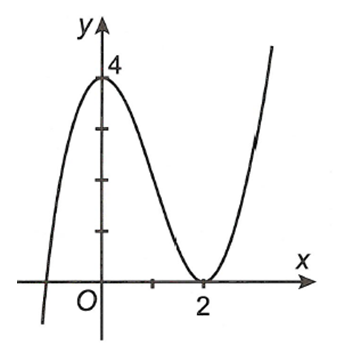
A. g(x) nghịch biến trên khoảng (0;2) .
B. g(x) đồng biến trên khoảng (−1;0)
C. g(x) nghịch biến trên khoảng (−12;0) .
D. g(x) đồng biến trên khoảng (−∞;−1) .

