Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d và một điểm O nằm ngoài cả hai mặt phẳng đó. Gọi A, B là hai điểm phân
16
08/10/2024
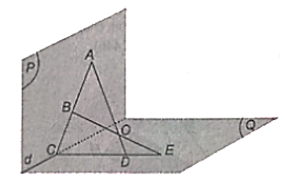
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d và một điểm O nằm ngoài cả hai mặt phẳng đó. Gọi A, B là hai điểm phân biệt thuộc mặt phẳng (P) sao cho AB cắt d tại C. Gọi D, E lần lượt là giao điểm của hai đường thẳng OA, OB và mặt phẳng (Q). Chứng minh rằng ba điểm C, D, E thẳng hàng.
Trả lời
Ta có C là giao điểm của hai đường thẳng AB và d nên C là một điểm chung của hai mặt phẳng (OAB) và (Q).
D là giao điểm của đường thẳng OA và mặt phẳng (Q) nên D là một điểm chung của hai mặt phẳng (OAB) và (Q).
E là giao điểm của đường thẳng OB và mặt phẳng (Q) nên E là một điểm chung của hai mặt phẳng (OAB) và (Q).
Do đó, ba điểm C, D, E đều thuộc giao tuyến của hai mặt phẳng (OAB) và (Q) nên ba điểm đó thẳng hàng.