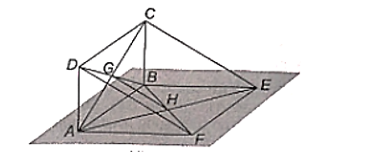
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song.