Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39). a) Tìm phép tịnh tiến biến đường tròn (O1) thành đường tròn (O2). b) Tìm phép đối xứng tâm biến đường tròn (O1
23
10/08/2024
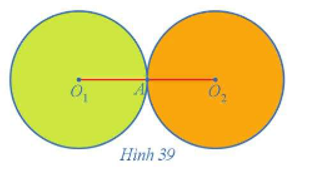
Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
a) Tìm phép tịnh tiến biến đường tròn (O1) thành đường tròn (O2).
b) Tìm phép đối xứng tâm biến đường tròn (O1) thành đường tròn (O2).
c) Tìm phép đối xứng trục biến đường tròn (O1) thành đường tròn (O2).
Trả lời
a) Hai đường tròn (O1; R) và (O2; R) có cùng bán kính. Ta có phép tịnh tiến theo vectơ biến điểm tâm O1 thành tâm O2.
Như vậy, phép tịnh tiến theo vectơ biến đường tròn (O1; R) thành đường tròn (O2; R).
b) Ta có: O1A = O2A = R nên A là trung điểm của O1O2. Do đó, có phép đối xứng tâm A biến O1 thành O2.
Như vậy, phép đối xứng tâm O biến đường tròn (O1; R) thành đường tròn (O2; R).
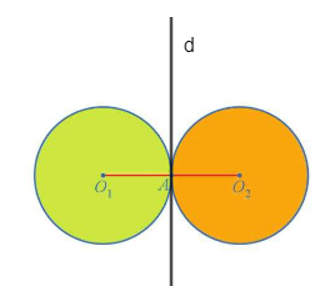
c)
Qua A, kẻ đường thẳng d vuông góc với O1O2. Khi đó đường thẳng d là đường trung trực của đoạn thẳng O1O2. Do đó, ta có phép đối xứng trục d biến O1 thành O2.
Như vậy, phép đối xứng trục d biến đường tròn (O1; R) thành đường tròn (O2; R).