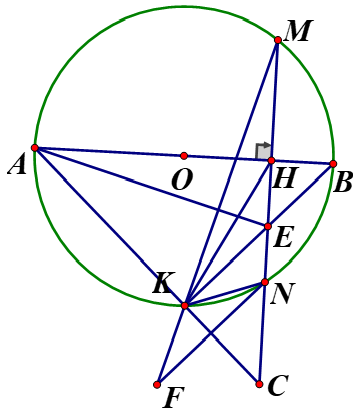
Cho đường tròn (O, R) Có đường kính AB vuông góc với dây cung MN tại H(H nằm giữa O và B) .Trên tia MN lấy điểm C
Cho đường tròn Có đường kính AB vuông góc với dây cung MN tại H(H nằm giữa O và B) .Trên tia MN lấy điểm C nằm ngoài đường tròn Sao cho đoạn thẳng AC cắt đường tròn tại điểm K khác A hai dây MN và BK cắt nhau ở E .
a) Chứng minh rằng : Tứ giác là tứ giác nội tiếp.
b) Chứng minh rằng đồng dạng
c) Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại . Chứng minh rằng là tam giác cân.